א. מבוא
מים יכולים להדליק נרות, האם זה נכון? זה נכון!
האם זה נכון שנחשים מפחדים מריאלגאר? זה שקר!
מה שאנחנו הולכים לדון בו היום הוא:
האם הפרעה יכולה לשפר את דיוק המדידה?
בנסיבות רגילות, הפרעות הן האויב הטבעי של המדידה. הפרעות יפחיתו את דיוק המדידה. במקרים חמורים, המדידה לא תתבצע כרגיל. מנקודת מבט זו, הפרעות יכולות לשפר את דיוק המדידה, וזה לא נכון!
אולם, האם זה תמיד המצב? האם יש מצב שבו הפרעה אינה מפחיתה את דיוק המדידה, אלא משפרת אותו?
התשובה היא כן!
2. הסכם התערבות
בשילוב עם המצב בפועל, אנו מגיעים להסכמה הבאה בנוגע להפרעה:
- ההפרעה אינה מכילה רכיבי DC. במדידה בפועל, ההפרעה היא בעיקר הפרעת AC, והנחה זו סבירה.
- בהשוואה למתח הישר הנמדד, משרעת ההפרעה קטנה יחסית. זה תואם את המצב בפועל.
- הפרעה היא אות מחזורי, או שהערך הממוצע הוא אפס בתוך פרק זמן קבוע. נקודה זו אינה בהכרח נכונה במדידה בפועל. עם זאת, מכיוון שההפרעה היא בדרך כלל אות AC בתדר גבוה יותר, עבור רוב ההפרעות, המוסכמה של ממוצע אפס סבירה לפרק זמן ארוך יותר.
3. דיוק מדידה תחת הפרעות
רוב מכשירי המדידה והמדים החשמליים משתמשים כיום בממירי AD, ודיוק המדידה שלהם קשור קשר הדוק לרזולוציה של ממיר ה-AD. באופן כללי, לממירי AD בעלי רזולוציה גבוהה יותר יש דיוק מדידה גבוה יותר.
עם זאת, הרזולוציה של AD תמיד מוגבלת. בהנחה שהרזולוציה של AD היא 3 סיביות ומתח המדידה הגבוה ביותר הוא 8V, ממיר ה-AD שווה ערך לסולם המחולק ל-8 חטיבות, כל חטיבה היא 1V. הוא 1V. תוצאת המדידה של AD זה היא תמיד מספר שלם, והחלק העשרוני תמיד נשא או מבוטל, מה שמניחים במאמר זה. נשיאה או פסילה יגרמו לשגיאות מדידה. לדוגמה, 6.3V גדול מ-6V וקטן מ-7V. תוצאת המדידה של AD היא 7V, ויש שגיאה של 0.7V. אנו קוראים לשגיאה זו שגיאת כימות AD.
לנוחות הניתוח, אנו מניחים שלקנה המידה (ממיר AD) אין שגיאות מדידה אחרות מלבד שגיאת הכימות של AD.
כעת, אנו משתמשים בשני סולמות זהים כאלה כדי למדוד את שני מתחי הזרם הישיר המוצגים באיור 1 ללא הפרעות (מצב אידיאלי) ועם הפרעות.
כפי שמוצג באיור 1, מתח הישר שנמדד בפועל הוא 6.3 וולט, ומתח הישר באיור השמאלי אינו חווה הפרעות, והוא ערך קבוע. האיור מימין מציג את הזרם הישיר המופרע על ידי הזרם החילופין, ויש תנודה מסוימת בערך. מתח הישר בתרשים הימני שווה למתח הישר בתרשים השמאלי לאחר ביטול אות ההפרעה. הריבוע האדום באיור מייצג את תוצאת ההמרה של ממיר ה-AD.

מתח DC אידיאלי ללא הפרעות
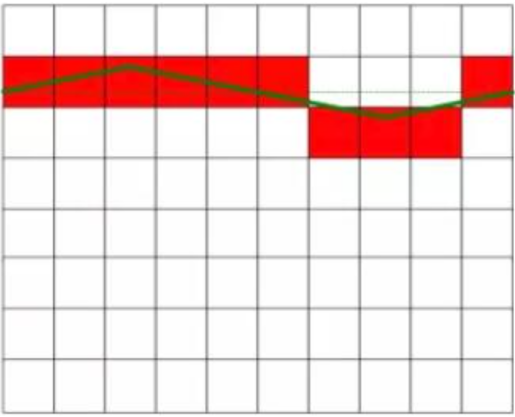
הפעל מתח DC מפריע עם ערך ממוצע של אפס
בצע 10 מדידות של הזרם הישיר בשני המקרים באיור לעיל, ולאחר מכן חשב את ממוצע 10 המדידות.
הסקאלה הראשונה משמאל נמדדת 10 פעמים, והקריאות זהות בכל פעם. עקב השפעת שגיאת הכימות של AD, כל קריאה היא 7V. לאחר חישוב ממוצע של 10 מדידות, התוצאה עדיין 7V. שגיאת הכימות של AD היא 0.7V, ושגיאת המדידה היא 0.7V.
הסקאלה השנייה מימין השתנתה באופן דרמטי:
עקב ההבדל במתח ההפרעה החיובי והשלילי ובאמפליטודה, שגיאת הכימות של AD שונה בנקודות מדידה שונות. תחת שינוי שגיאת הכימות של AD, תוצאת מדידת AD משתנה בין 6V ל-7V. שבע מהמדידות היו 7V, רק שלוש היו 6V, והממוצע של 10 המדידות היה 6.3V! השגיאה היא 0V!
למעשה, אין טעות שאינה אפשרית, כי בעולם האובייקטיבי, אין 6.3V קפדני! עם זאת, אכן ישנם:
במקרה של אין הפרעה, מכיוון שכל תוצאת מדידה זהה, לאחר חישוב ממוצע של 10 מדידות, השגיאה נשארת ללא שינוי!
כאשר ישנה כמות מתאימה של הפרעות, לאחר חישוב ממוצע של 10 מדידות, שגיאת הכימות של ה-AD מצטמצמת בסדר גודל! הרזולוציה משתפרת בסדר גודל! גם דיוק המדידה משתפר בסדר גודל!
השאלות המרכזיות הן:
האם זה אותו הדבר כאשר המתח הנמדד הוא ערכים אחרים?
ייתכן שקוראים ירצו לעקוב אחר ההסכמה על הפרעות בסעיף השני, לבטא את ההפרעה בסדרה של ערכים מספריים, להניח את ההפרעה על המתח הנמדד, ולאחר מכן לחשב את תוצאות המדידה של כל נקודה לפי עקרון הנשיאה של ממיר ה-AD, ולאחר מכן לחשב את הערך הממוצע לאימות, כל עוד משרעת ההפרעה יכולה לגרום לשינוי בקריאה לאחר כימות ה-AD, ותדר הדגימה גבוה מספיק (לשינויים במשרעת ההפרעה יש תהליך מעבר, ולא שני ערכים של חיובי ושלילי), ויש לשפר את הדיוק!
ניתן להוכיח שכל עוד המתח הנמדד אינו מספר שלם בדיוק (הוא אינו קיים בעולם האובייקטיבי), תהיה שגיאת קוונטיזציה של AD, לא משנה כמה גדולה שגיאת הקוונטיזציה של AD, כל עוד משרעת ההפרעה גדולה משגיאת הקוונטיזציה של AD או גדולה מהרזולוציה המינימלית של AD, היא תגרום לתוצאת המדידה להשתנות בין שני ערכים סמוכים. מכיוון שההפרעה סימטרית חיובית ושלילית, הגודל וההסתברות לירידה ולעלייה שווים. לכן, כאשר הערך בפועל קרוב יותר לערך מסוים, ההסתברות להופעת הערך מסוים גדולה יותר, והוא יהיה קרוב לערך מסוים לאחר מיצוע.
כלומר: הערך הממוצע של מדידות מרובות (ערך ממוצע ההפרעה הוא אפס) חייב להיות קרוב יותר לתוצאת המדידה ללא הפרעות, כלומר, שימוש באות הפרעת AC עם ערך ממוצע של אפס וממוצע של מדידות מרובות יכול להפחית את שגיאות הכימות של AD המקבילות, לשפר את רזולוציית מדידת AD ולשפר את דיוק המדידה!
זמן פרסום: 13 ביולי 2023




